By Yiyu Chen
First, we have point correspondences of two relate images. And then try to apply homography on one to project them into same plane.

Homography is a 3x3 transformation matrix used in image processing to map points from one plane to another, typically from one image to another. This transformation can include translation, rotation, scale, and perspective distortion. A homography matrix \(H\) can be represented as follows:
\[H = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & 1 \end{bmatrix}\]
To compute the homography matrix using point correspondences, we start with pairs of matched points \( (x, y) \) from one image and \( (x', y') \) from another image. The relationship between these points through the homography matrix \( H \) is given by:
\[ \begin{bmatrix} wx' \\ wy' \\ w \end{bmatrix} = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \]
Expanding and rearranging, we get two equations for each point pair:
\[\left\{ \begin{align*} ax + by + c &= wx' \\ dx + ey + f &= wy' \\ gx + hy + 1 &= w \end{align*} \right. \]
\[ \Rightarrow \left\{ \begin{align*} &ax + by + c - gx' - hy' = x' \\ &dx + ey + f - gx'y - hy'y = y' \end{align*} \right. \]
Stacking these equations to matrix form:
\[ \begin{bmatrix}\ x' \\ y' \end{bmatrix} = \begin{bmatrix} x & y & 1 & 0 & 0 & 0 & -x'x & -x'y \\ 0 & 0 & 0 & x & y & 1 & -y'x & -y'y \end{bmatrix} \begin{bmatrix} a \\ b\\ c\\ d\\ e\\ f\\ g\\ h \end{bmatrix} \]
Although the matrix can be computed with as few as four points at a minimum, to minimize the error, we provide more pairs of points to the function. The system becomes overdetermined, meaning there are more equations than unknowns. This is typically solved using the least squares method, which minimizes the sum of the squares of the residuals (the differences between the observed values and those predicted by the model). Mathematically, the least squares solution is given by:
\[ \hat{h} = (A^ \top A)^ {-1} A ^ \top b\]
After obtaining the solution, add 1 to the back and reshape to 3x3. Then we get homography.
Make rectangular objects looks rectangular using a homography matrix.




Here, we take two images and their correspondences as input. We compute the homography matrix and then expend the canvas according to the four corner points of the warped image and base image.



If we simply average the two images where they overlap, we would see the edge artifacts. To make the blend smoother, I used bwdist to compute a distance map and applied a Laplacian pyramid using mask from the distance map.

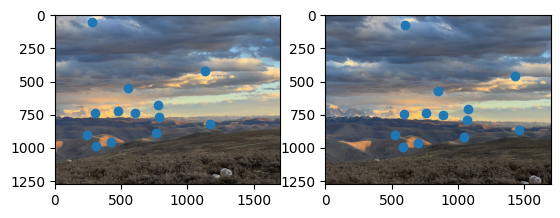
Terrace Entrance



Sunset




Use Harris corner detector to detect corners in the image. The Harris corner detector is a method used to extract corners from an image. It is based on the idea that corners can be detected by looking for significant changes in intensity in all directions. However, Harris corner points are very dense and don't lend themselves to subsequent processing.


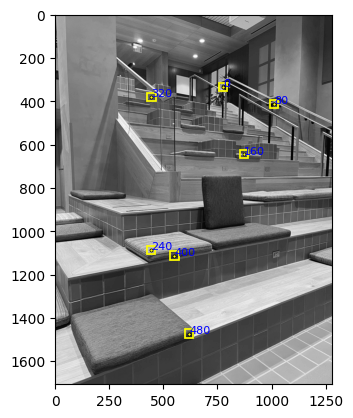
To remove redundant information from the corner points, I apply ANMS to reduce the number of interest points. It works by selecting the most significant corners and discarding the rest. The algorithm works by sorting the corners by their Harris response and then iterating through the list to find the minimum distance to a corner with a higher response. If the distance is greater than a threshold, the corner is kept; otherwise, it is discarded. This process is repeated until the desired number of corners is reached.This algorithm results in a more even distribution of points comparing to direct select the maximize point by order.

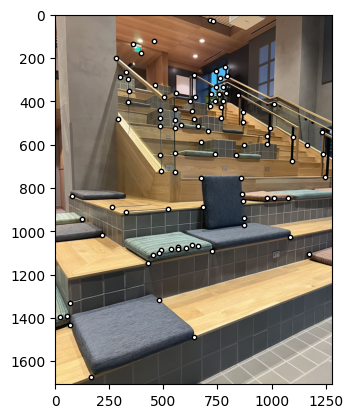
I first extracted the 40x40 subsample from the corners returned by ANMS and then reduced the sampling rate to get an 8x8 feature subsample. Here I show visualizations of features of a few random corner points:
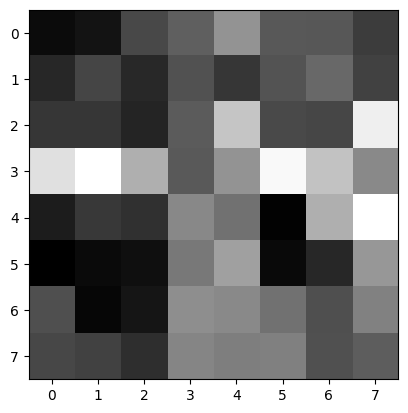
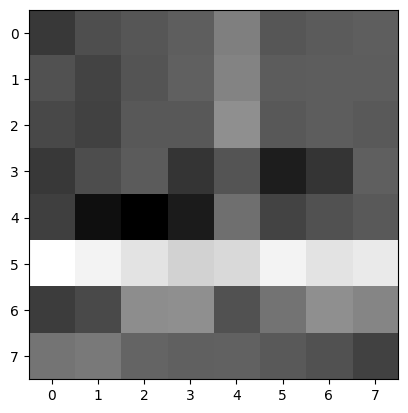
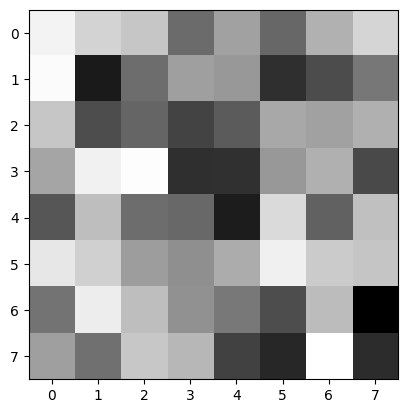
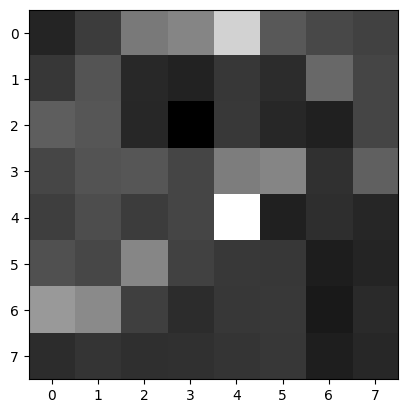
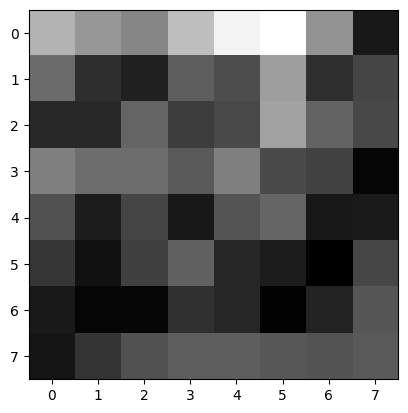
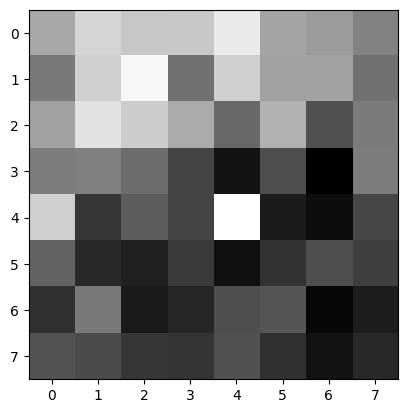
Use the Euclidean distance between the feature vectors to find the best match. The best match is the one with the smallest Euclidean distance. For each corner, I flatten its features and then compute the best match (first nearest neighbor) and the second best match (second nearest neighbor) in the other group. I then apply Lowe's technique: calculate the 1-NN and 2-NN errors and the e1-NN/e2-NN ratio, then apply a threshold, and if the ratio is less than the threshold, we use that best matching pair.
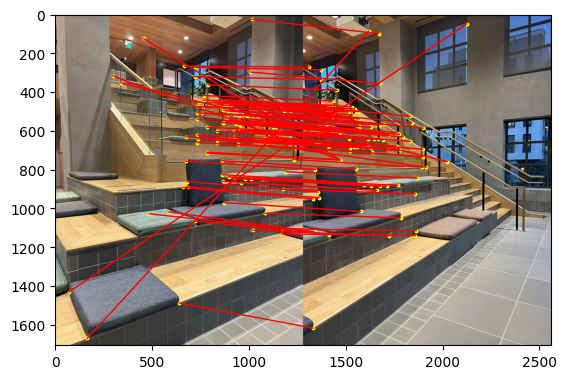
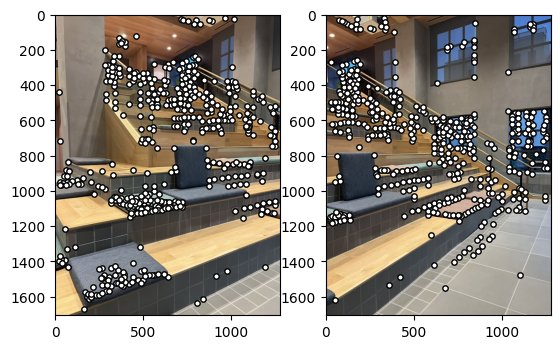
Here is the matches pairs after Lowe's technique. We can see most of the points corresponded visually correctly, with only a few corners showing an obviously incorrect match.
RANSAC (Random Sample Consensus) is a very powerful iterative method for identifying outliers in data and estimating the parameters of a mathematical model from the remaining interior points. Its basic steps include:
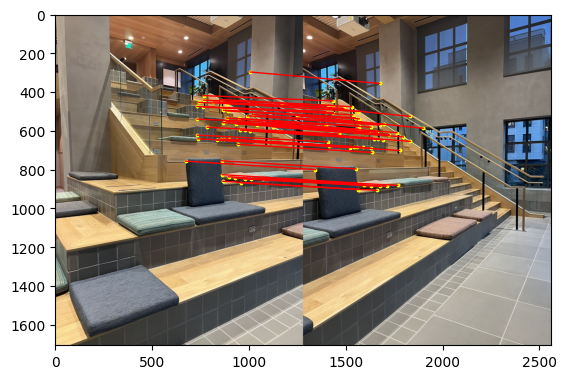
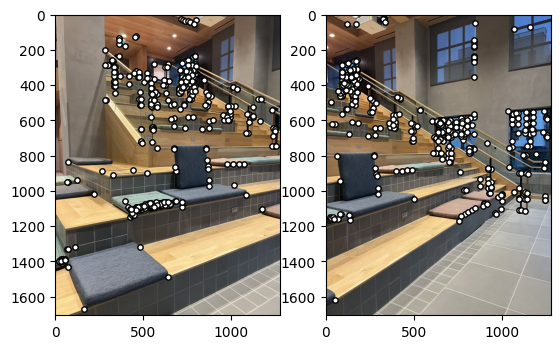
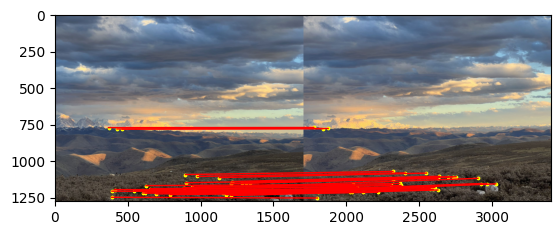
Here is the result of RANSAC. We can see the inliers are correctly matched and the outliers are removed.
Take all these inliers, recompute the homography matrix. After that, we can warp the image and blend them together. Here is the result of the mosaics.



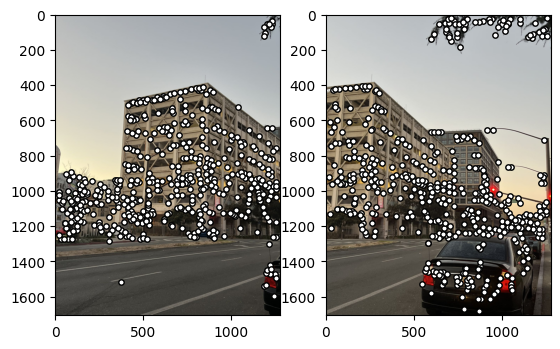
Street




Sunset
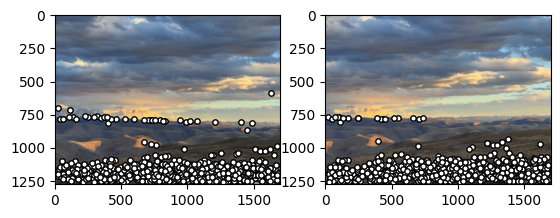
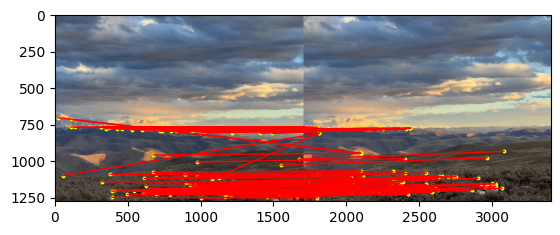


For the street pictures, the manual and automatic correspondences yielded very similar results. For sunsets, there are some minor differences, but they all work well. I suspect the reason for this is that when manually selecting correspondences, I tend to choose the point in the center of the image, but since there are few corner points detected in the sky in the upper part of the image, the automatic correspondences tend to concentrate on the lower part of the image, where the grass is, since the corners are more prominent here.
At the same time, I have observed that for images with distinct corner features, such as steps and buildings on the street, most automatically detected corners are located in the central area of the image. This corresponds to the distortion characteristics of the camera. That is to say, the middle part of the image tends to retain its original structure, while the edges of the image are somewhat distorted. The edges are difficult to maintain correspondence between the two images due the distortion is nonlinear, but the center retains better correspondence.
I think it's cool to automate point extraction. Because in past projects, I realized the importance of alignment in computer vision, but I've been manually extracting the correspondness, and it's been bugging me. What's even cooler is that in this project, we don't need hard skills or arithmetic to automate the process. While our eyes have been dominated by cutting-edge, complex theories, it's amazing to see these simple algorithms quickly get the job done so well.